三角錐の体積 =底面積×高さ×(1/3) = abd×ac×(1/3) =8㎤ 2.三角錐の表面積の求め方 三角錐の側面は、全て三角形です。したがって、三角形の面積を求める方法を四か所で行うことで、必然的に三角錐の表面積を求めることができます。四角錐 ⇒ (上底下底)÷2×高さ×四角柱の高さ÷3 三角錐 ⇒ 底辺×高さ÷2×三角柱の高さ÷3 体積の求め方、覚え方 体積の公式の覚え方は簡単です。 球の体積を除けば、たった2つの公式を覚えるだけで済三角錐の体積=底面積 高さ 三角錐の体積を求めるときに気をつけたいのは、 必ず を掛ける ことです。

3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ
三角錐 体積 求め方 高校
三角錐 体積 求め方 高校- 第4講「図形の計量」(4)球の体積と表面積(その3/3) 「(佐藤の)数学教科書三角比・平面図形編」(東進ブックス)の学習 練習問題231辺の長さがaである正四面体について、次の問に答えなさい。 (3)この正四面体に内接する球の半径rを求めなさい。 教科書の解き方が三角錐の体積は底面積 ️高さ 3なので、高さが同じであれば底面積の比が体積比となります。 ななせ 3年以上前 ありがとうございます! この回答にコメントする




中学数学 円錐の表面積の求め方と公式 図たくさん なぜか分かる はかせちゃんの怪しい研究室
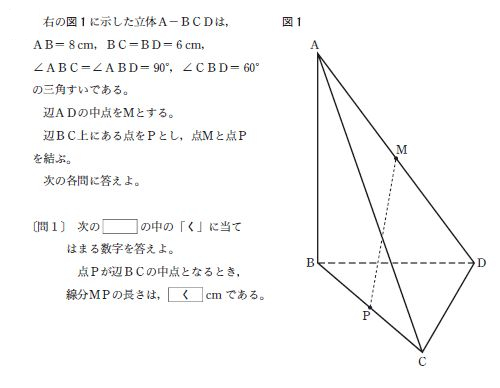
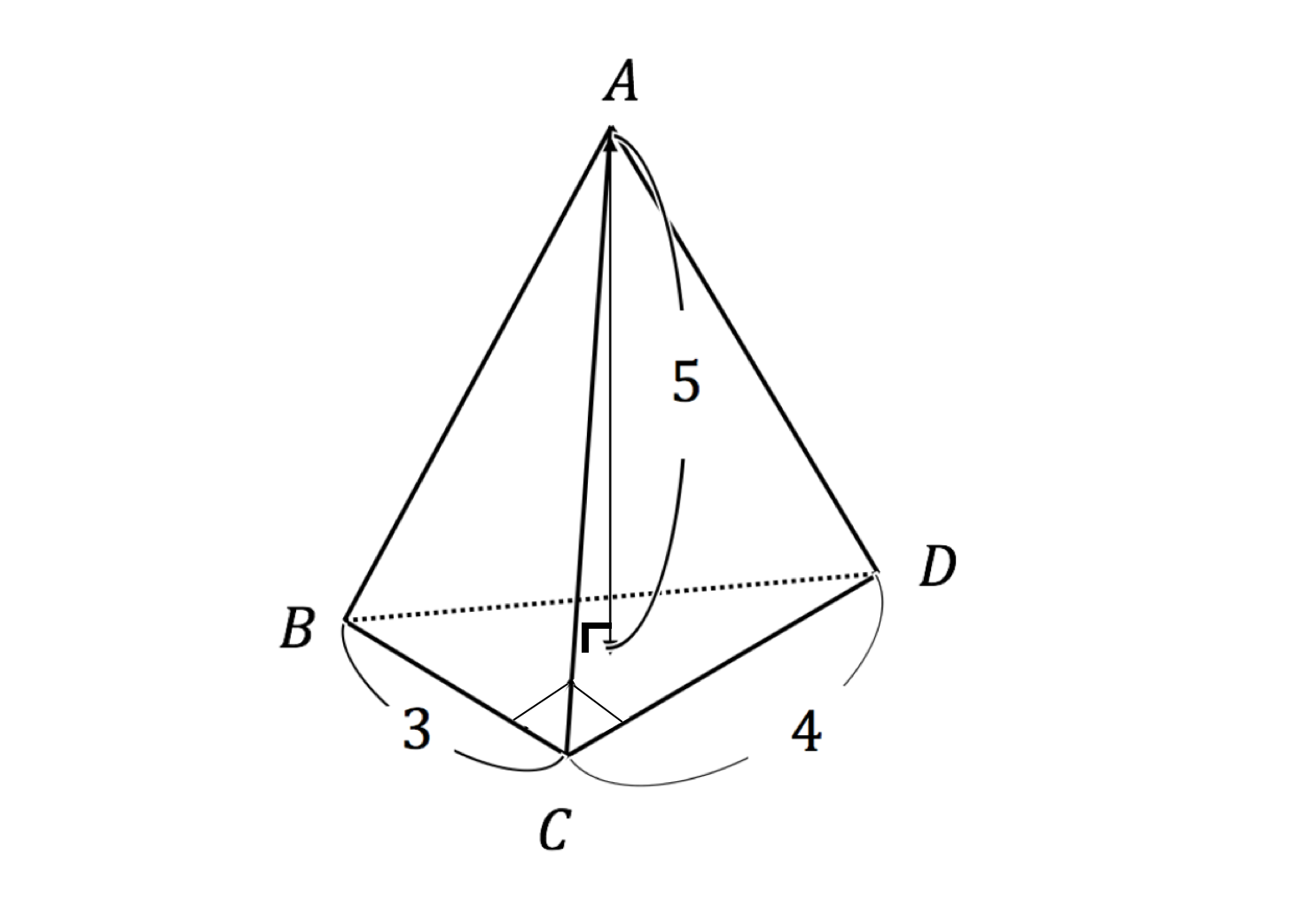
すると四角錐kaefj と三角錐kefh に分かれる。 四角錐は台形aefj を底面として高さがak なので (26)×6÷2×2÷3=16 体積16cm 3 三角錐は efh が底面で kから面efghにおろした垂線の長さが高さである。 よって体積は6×6÷2×6÷3=36 よって3616=52 となる まとめ:円錐の体積の求め方の公式はシンプル 円錐の体積の求め方はどうだったかな?? 底面積×高さ×1/3 という公式は意外とシンプルだったよね笑 最後に1/3をかけることさえ忘れなければ、ぜったいにテストでも間違えないはず。 そのため、CD=6cmと分かります。 PとHがそれぞれBCとBDの中点なので、中点連結定理よりPH=CD÷2=6÷2=3cmです。 MPHに三平方の定理を用いて、MP 2 =MH 2 +PH 2 =4 2 +3 2 =25よりMP=5cmです。 例年、大問5の 問1は平易な問題が出題されます。 しかし、平成29年度は、補助線を引かなければならないため、やや複雑でした。 正答率が338%だったのは、
最初に注目するのは底面の正方形です。 このように底面の対角線を引いて、その長さを求めます。 すると45°、45°、90°の直角三角形ができるので の比になりますね。 そこから、対角線の長さは さらに、その半分の長さ まで求めておきましょう。 次に、正四角錐の高さを含む こちらの直角三角形に注目します。 すると、先ほど求めた ㎝ の辺を用いて高校生 数学 この問題の解き方が分かりません。 教えてくださると助かります🙇♀️ ちなみに解答は (1)7通り (2)3600通り です。 高校生 数学 なんでodベクトル=4×nベクトル/nベクトルの大きさ にしているのか教えてください! 解答の上から7行目 三角錐の重心(四面体の重心) 高校数学 立体図形 「 三角錐 の重心Oの位置は、その高さの4分の1になります。 」 以下に、 三角錐 の重心の性質の簡単な求め方を示します。 上の図のように、 三角錐 の重心を3次元座標の原点Oにして考えます。 三角錐 ABCDの頂点の座標の平均 (A+B+C+D)/4 が 三角錐 の重心です。
簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ 計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく 三角錐 四角錐 円錐の体積を求める公式と例題 具体例右図のように点 Q を通り ABC に平行な平面と AD, CF の交点を S, T とおくとき,三角柱 SQTDEF ,三角すい PSQT ,三角すい PQTR の3つに分けて体積を求めるとよい. 底面 ABC の面積は, 4×6÷2=12 だから,三角柱 SQTDEF の体積は 三角すい PSQT は SQT=12 を底面とすると, PS=1 が高さになるから 三角すい PQRT は QRT=6×4÷2=12 を底面とすると, QS=4 が高さになる.そ三角錐,四角錐,円錐などの錐体の体積は 1 3 \dfrac{1}{3} 3 1 ×底面積×高さ 底面積が S S S ,高さが h h h である錐体の体積 V V V を求める公式: V = 1 3 S h V=\dfrac{1}{3}Sh V = 3 1 S h の導出を紹介



Mathematics 錐体の一部の体積 働きアリ




中学数学 円錐の表面積の求め方と公式 図たくさん なぜか分かる はかせちゃんの怪しい研究室
三角錐の体積 当HPの読者のK.S.さんより、平成24年10月10日付けで標記話題をメールで頂いた。 原点をOとし、空間上の3点A(a 1 ,a 2 ,a 3 )、B(b 1 ,b 2 ,b 3 )、C(c 1 ,c 2 ,c 3 )とす 計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを 円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生 体積の求め方 計算公式一覧 中1数学 三角すい 四角すいの体積の求め方がサクッとわかる 映像 相似比と体積の計算三角錐の体積と表面積の求め方!計算プロセスがよくわかる 三角錐の体積と表面積の求め方!計算プロセスがよくわかる図形のイラスト付き 今回学習する三角錐は、中学生で学習する図形の中でも比較的難しい範囲だとされます。




錐 すい の体積と三角形の面積 数学のカ
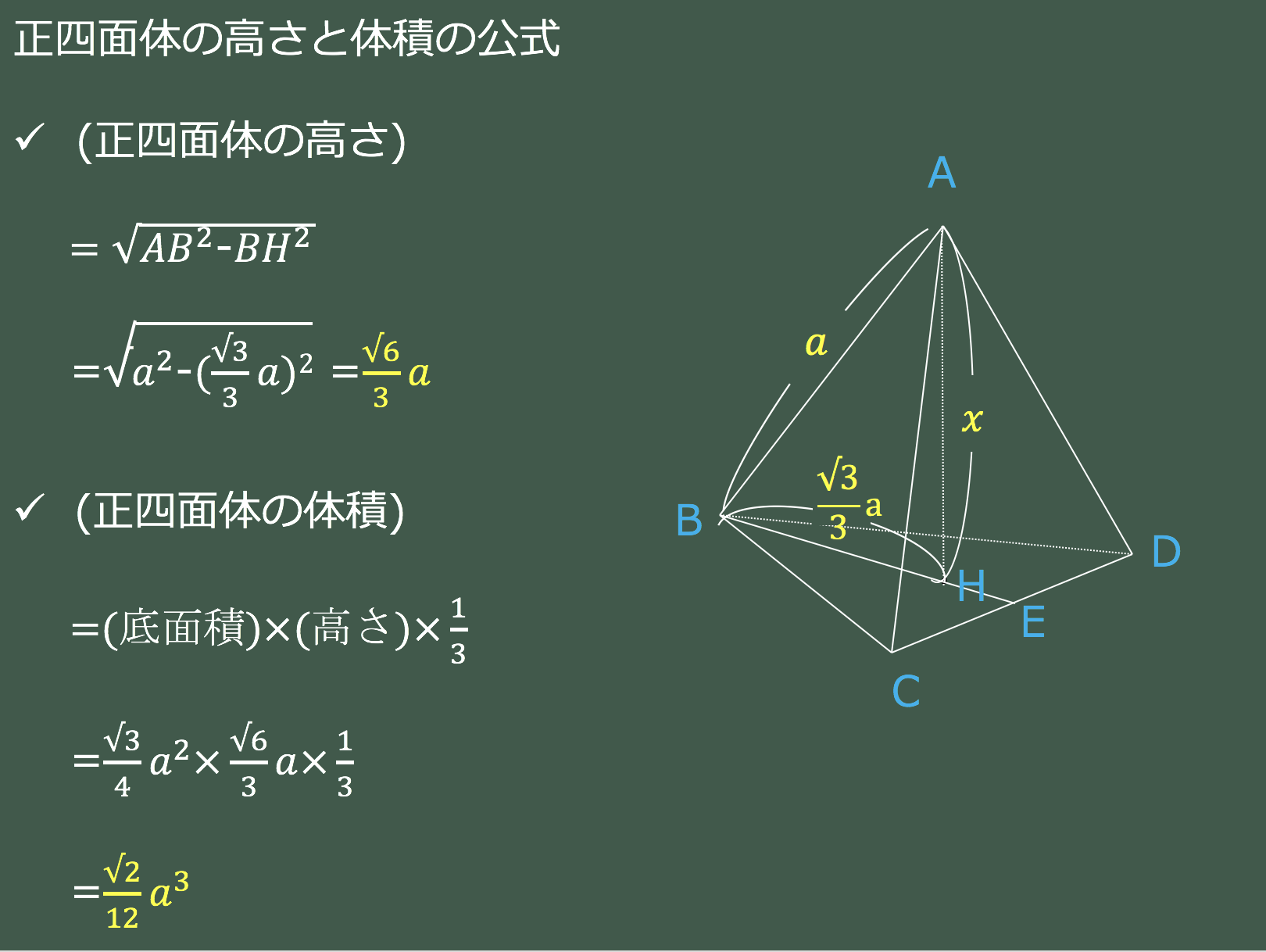



3分で分かる 正四面体の高さ 体積の求め方をわかりやすく 合格サプリ
この記事の目的:錐形を求める際に「3分の1」する理由を中学生にも分かるように説明する. はじめに 錐形は3分の1 指針 ①特別な四角錐を考える ②特別な三角錐を考える ③錐体の体積の求め方の根本を考える ④体積が変わると? 最後に正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積 くさび形の体積 角錐台の体積 角錐の体積 直円柱の体積 一部が欠けた直円柱の体積 中空円柱の体積 斜切円柱の体積 楕円柱の体積 直円錐の中学1年 資料の整理 (活用) 有効数字とは、信用できる数字の桁(けた)数のことです。 ここでは中学の資料の整理・活用の範囲での四捨五入と桁数について有効数字の使い方、表し方を説明します。 足し算やかけ算などの計算が関係する有効数字は高校



三角錐の体積の公式は 1分でわかる公式 問題 底面積との関係
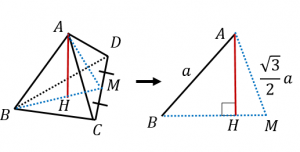



正四面体の高さと体積の求め方 具体例で学ぶ数学
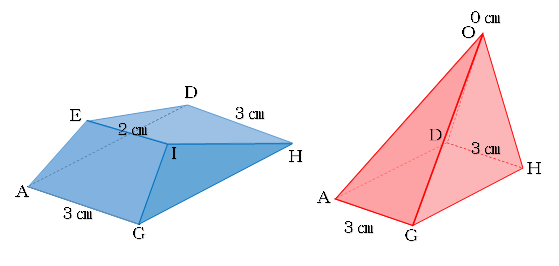
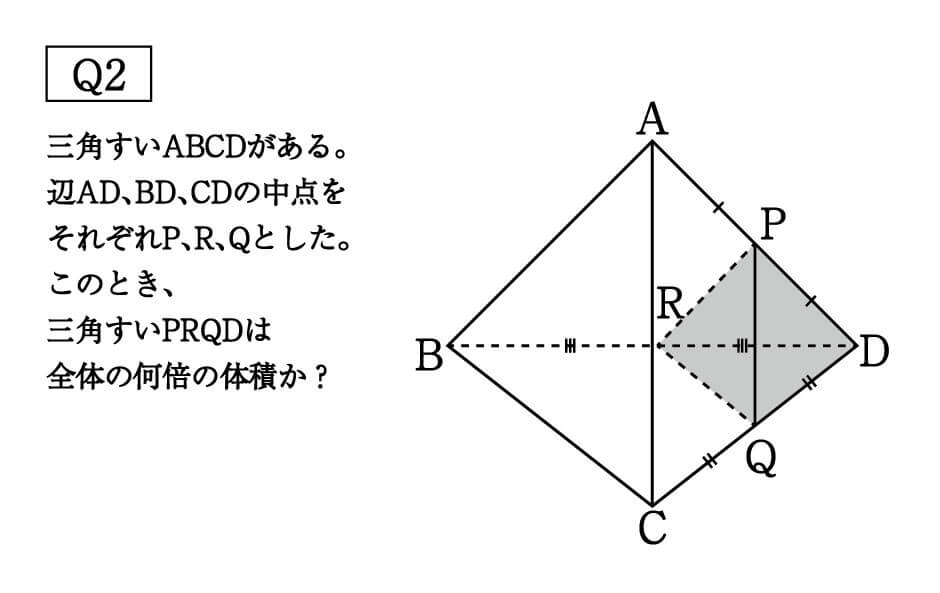
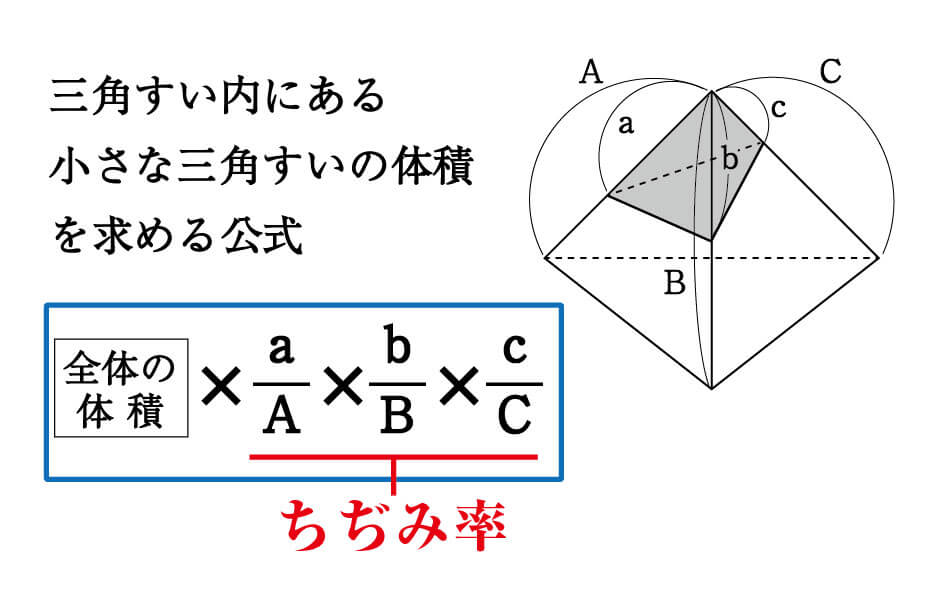
よって、底面積比が \(13\) で、高さの比が \(12\) なので、体積の比は、 \(1×13×2=16\) つまり、この切断によって得られる立体のうち、点 \(O\) を含む方は、もとの立体の体積の \(\displaystyle \frac{1}{6}\) 倍です。 以上求まりました スポンサーリンク三角錐abcdが、 bcdを底面にして、机の上に置かれている。辺の長さをそれぞれ、 ab=1、ac= 、ad= 、bc= 、bd= 、cd=3 とする。このとき、三角錐abcdの体積を求めよ。 (答) 1/2 よおすけさんになりかわって解いてみた。 /2 よって、 ABDを底面とする「正四面体」 、つまり 「三角すい」 の体積を求めるよ。先のとがった、「すい」の体積の求め方って覚えているかな? (「すい」の体積)= (底面積)×(高さ)×1/3 だったね。 をするところに注意だ。




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
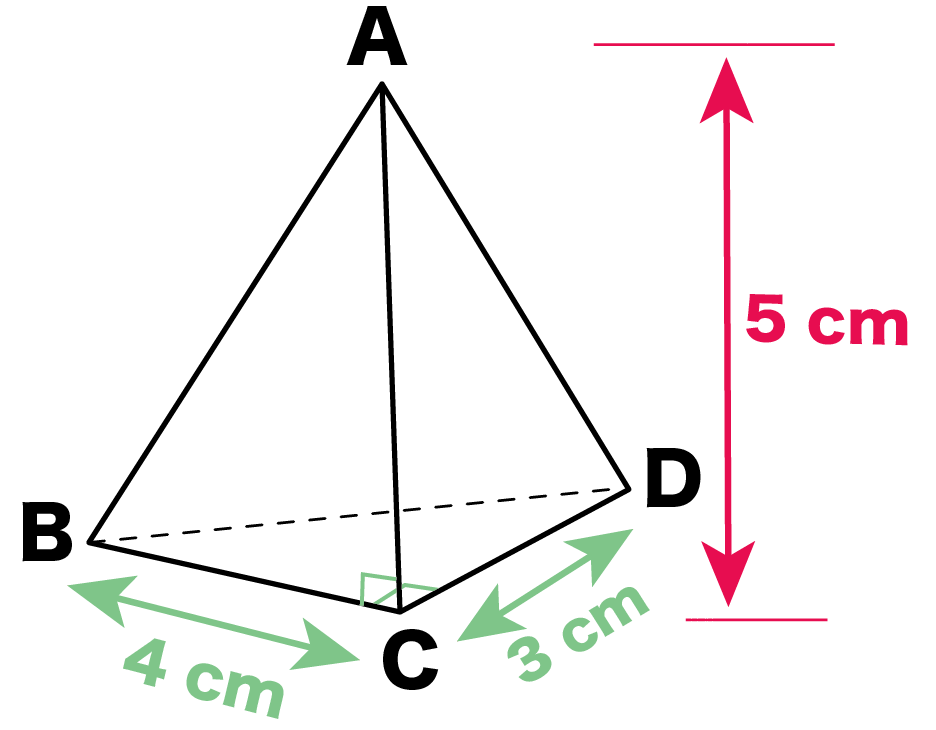
三角錐の体積の公式は (三角錐の体積)=(底面積)×(高さ)×\(\frac{ 1 }{ 3 }\) でしたね。 まずは、 底面積(三角形\(BCD\)) を求めます。 \((三角形BCD)=3×4×\frac{ 1 }{ 2 }=6\) 1 回答 高校一年の数学Ⅰの三角錐の体積を求める問題です。 問題PA=PB=PC=4、AB=6、BC=4、CA=5である三角錐PABCの体積Vを求めよ。 高校一年の数学Ⅰの三角錐の体積を求める問題です。 問題PA=PB=PC=4、AB=6、BC=4、CA=5である三角錐PABCの体積Vを求めよ。 底面積までは15√7/4と求めれたのですが体積を求めるための高さがわかりません。今日は、この公式で体積を計算してみよう!! 使って覚えるのが一番だからね。 三角錐の体積の求め方がわかる3ステップ 3ステップで計算できるよ。 底面積をだす 高さをかける 「3」でわる つぎの三角錐の体積を求めてみよう。 三角形の面積を計算する




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室




体積の求め方 計算公式一覧
体積・表面積 立方体の辺の長さから体積と表面積を計算します。 立方体の体積から辺の長さと表面積を計算します。 直方体の三辺の長さから体積と表面積を計算します。 四面体の6つの辺の長さから体積と表面積を計算します。 正四面体の辺の長さから体積と表面積を計算します。 正四面体の体積から辺の長さと表面積を計算します。 正三角柱の底辺と高さ小問(1) :三角錐台の体積の求め方 台形が出てきたら、 補助線を引くことがポイント です。 図bのように補助線を引くことで、三角すいとして考えることができます。 よく使う考え方ですので、しっかりと覚えておきましょう。 図b ≪三角錐台の体積の 体積の公式から高さの公式を導き出します。三角錐の高さを求めるには、ピラミッドの体積に3を掛け、得られた値をベース面積で除算する必要があります。h = 3V / S 3 三角錐の底辺は三角形なので、この式を使用して三角形の面積を計算します。




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学
三角錐の体積の求め方 には公式があるよ。 底面積をS、高さをhとすると、 三角錐の体積は、 1/3 Sh になるんだ。 つまり、 (底面積)×(高さ)÷ 3 ってわけだね。 今日は、この公式で体積を計算してみよう!角柱・角錐・円柱・円錐の体積の求め方がわかりません。公式を教えてください。 進研ゼミからの回答 立体の体積はこれから先も利用するので,それぞれしっかり覚えておきましょう。 ※ このQ&AではV = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S 1 = 角錐底面積 S 2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体



1




三角錐の体積と垂線の長さ Youtube
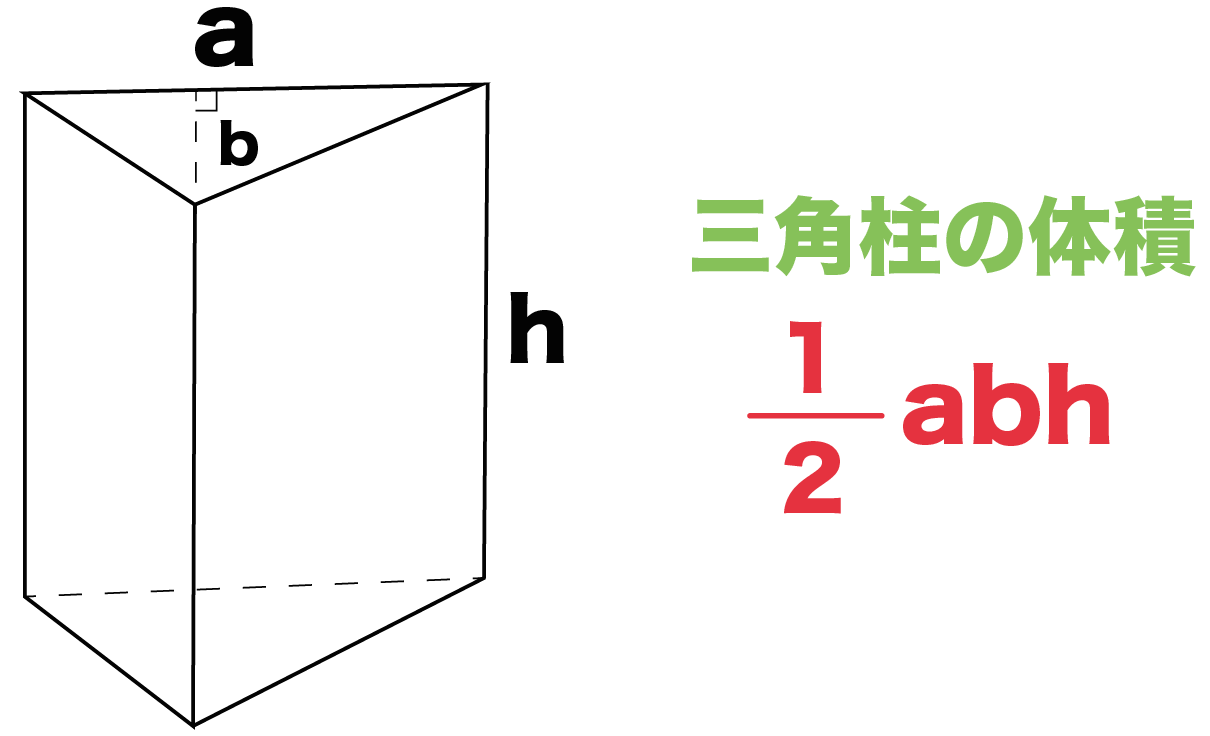
多面体の体積は、 「その立体をどう捉えるか」 によって簡単に求められたり、逆に面倒になったりします。世の中の出来事を、 「多様な面から捉える力」 を養うためにも、このような初等幾何への取り組みも一つの訓練になるでしょう。下記は、今年のある高校の入試問題です。三角錐OAEF=三角錐AOEF より,求める体積は9cm3 (3)体積を表す式から高さを求める (2)より,三角錐OAEF=9cm3 と求められているので, 三角錐OAEFの頂点Oから面AEFに下ろした垂線の長さを xとおくと, AEF×x× 1 3 =9cm3 となる。 (1)より, AEF = 27 2 だから, 27 2 ×断面の三角形の辺の長さは容易に 三角錐の体積の求め方 には公式があるよ。 底面積をS、高さをhとすると、 三角錐の体積は、 1/3 Sh になるんだ。 つまり、 (底面積)×(高 三角柱の体積の求め方の公式って?? こんにちは!この記事をかいているKenだよ。
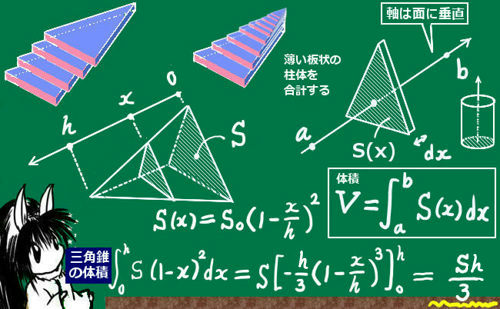



立体の体積計算 積分 高校 理数系無料オンライン学習 Kori




Hd限定円錐 体積 求め方 裏ワザ 最高のぬりえ
三角錐の体積の求め方積分 三角錐の体積 三角錐の体積算術 三角錐の行き当たりばったり体積=脂底面積×高せいこうさ× 証明 三角柱をダラス3つの三角錐に分解するこにっこりとで証明する. (Ⅰ)三角錐 含めてと三角錐 につ宣言済みいて 三角柱鹿 の阻ま錐体の体積に1 3がつくことの2 高校3年生のめいから質問された問題です。問題文は下記の図の通りです。この中で最後の三角錐OMPQの体積の求め方が分かりません。それまでの問いの答えから、 OM=3、OP=2、OQ=4、MP=√7、MQ=√13、PQ=2√3と思いま 数学 締切済 教えて!goo




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学
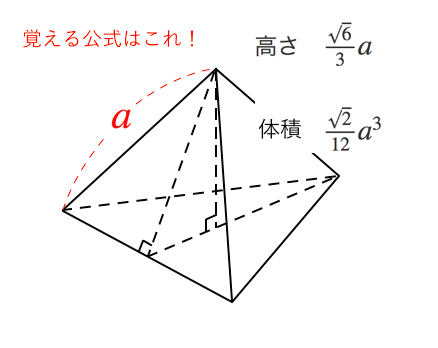



正四面体 高さ 面積を求める公式 苦手な数学を簡単に
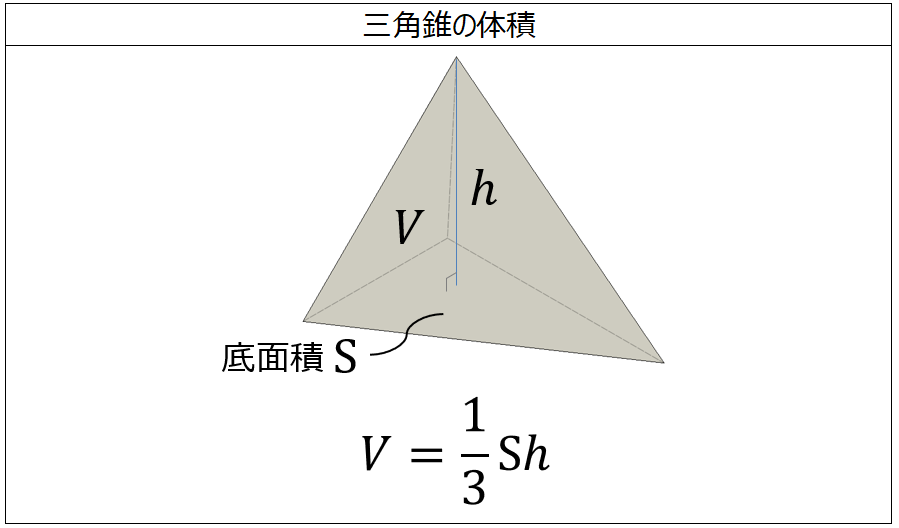



体積の計算 三角錐 製品設計知識




三角錐 体積 計算
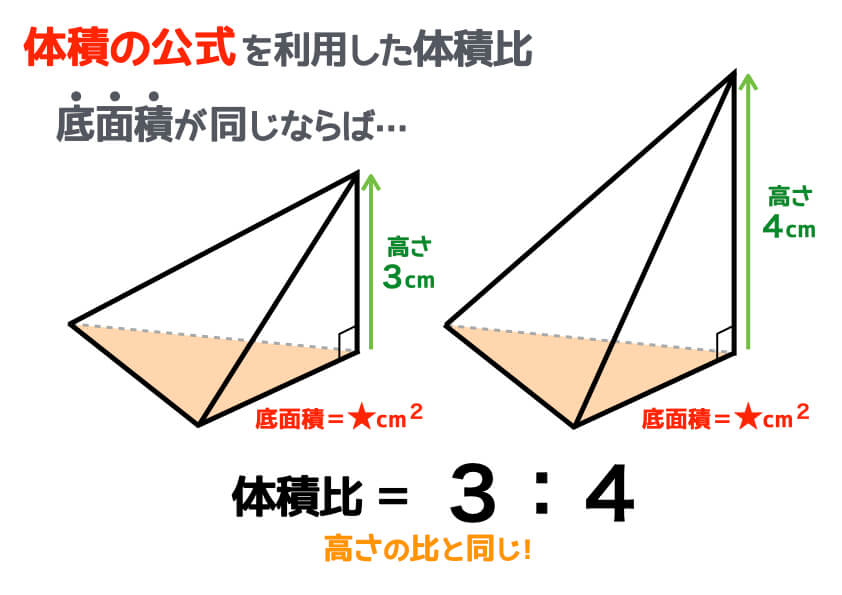



三角錐 体積比 求め方




中1数学 三角すい 四角すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




中学 数学 テクニック 三角錐の体積比 高校入試 高校受験 裏ワザ Youtube



高校数学の問題です 大きい三角錐の体積の求め方は分かりました Yahoo 知恵袋




数学 三角錐の体積比を楽に求められる公式 受験の秒殺テク 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



48s96ub7b0z5f Net Kuukan Bekutoru Taiseki 2




円錐や角錐の体積の求め方 中学1年数学 Youtube




高校数学 正四面体の高さと体積 練習編 映像授業のtry It トライイット




中1数学 三角すい 四角すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




3分でなるほど 三角錐の体積 表面積の求め方をマスターしよう 数スタ



一辺が12cmの立方体の中にある三角錐の体積の求め方を教えてく Yahoo 知恵袋




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




三角柱の体積 表面積の求め方が図で誰でも即わかる 展開図も紹介 高校生向け受験応援メディア 受験のミカタ




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題




円錐の体積ってなんであの公式なの Webty Staff Blog




角柱 円柱の表面積と体積の公式 数学fun




角錐 円錐の体積と表面積の公式 数学fun




高さの分からない正四角錐の体積を求める方法をイチから解説 数スタ




公式を図解 すい体の体積 円すいの表面積の求め方




簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



悲しき角錐の体積公式 1 3 がつく理由を中学数学で説明できる バナッハ タルスキーの定理 4 Youtube




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト



都立高校入試過去問解説 高さがわからない三角錐の体積を求めよう みみずく戦略室




円錐の体積の求め方 公式と計算例




半径5分の12cm 高さ6cmの双円錐の体積を求めるのに Clear




簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ




三角錐の体積と表面積の求め方 計算プロセスがよくわかる図形のイラスト付き




高校数学 3辺の長さが等しい 三脚型 四面体の体積 受験の月




公式を図解 すい体の体積 円すいの表面積の求め方



1




三角錐 四面体 の体積の公式 Schoolmath S Diary




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ




錐体の体積に1 3がつくことの2通りの説明 高校数学の美しい物語




中1数学 三角すい 四角すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット
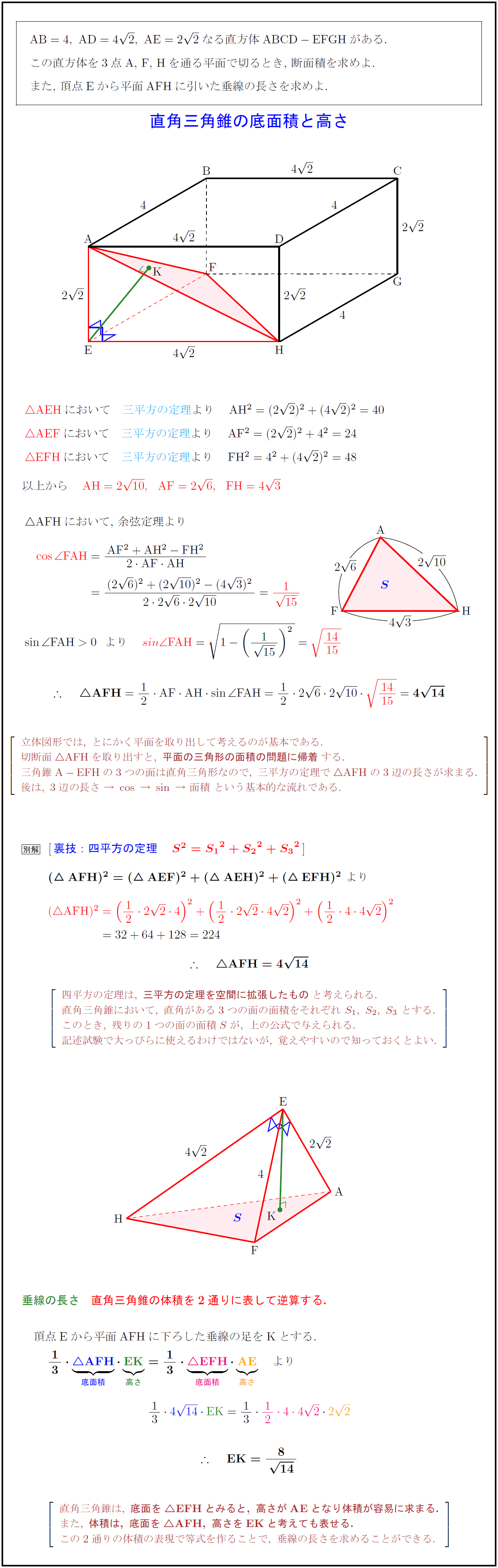



高校数学 直角三角錐 3直角四面体 の底面積と高さ 裏技 四平方の定理 受験の月




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun



第9回 立体図形必勝法 角すいの切断 算数ドクター




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト
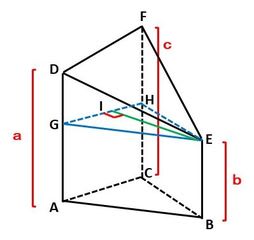



切断三角柱の体積の求め方 東久留米 学習塾 塾長ブログ




四角錐台の体積 高精度計算サイト




3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




中学数学 三角錐の高さの求め方がわかる4つのステップ Qikeru 学びを楽しくわかりやすく




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



公立高校入試2017 三角錐 中学から数学だいすき




簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ
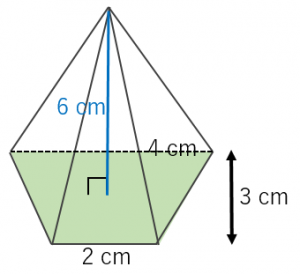



三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学
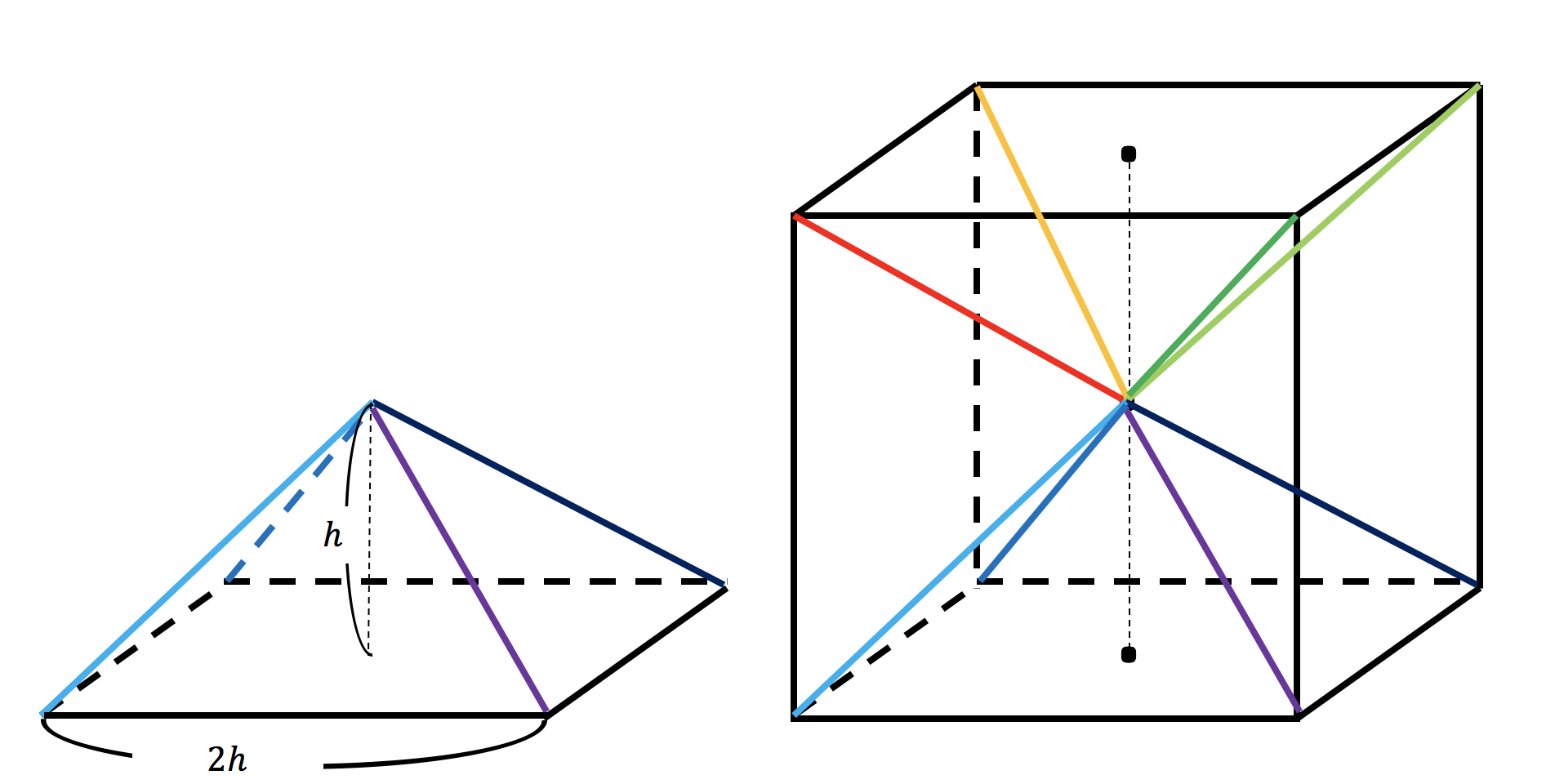



3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ




円すい 円錐 の体積の求め方と問題 小学数学 Irohabook
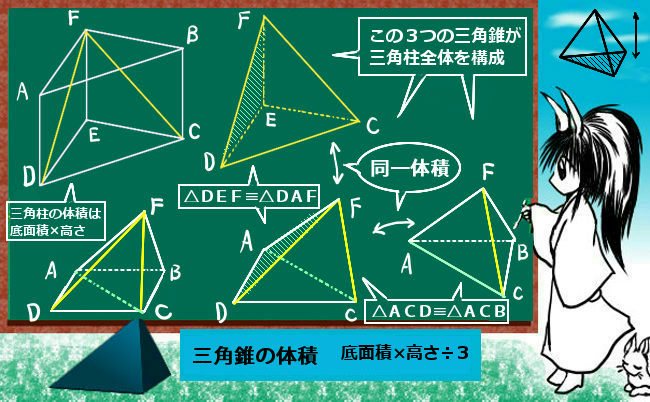



立体の体積 理数系無料オンライン学習 Kori




公式を図解 すい体の体積 円すいの表面積の求め方



簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



正四面体とは 高さ 体積 表面積の公式や求め方 受験辞典




三角錐 体積



計算公式 三角柱の体積の求め方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく




計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



数学 三角錐の体積比を楽に求められる公式 受験の秒殺テク 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



数学 三角錐の体積比を楽に求められる公式 受験の秒殺テク 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




空間図形14 円すい台の体積 Youtube



しょうちゃん 公式ブログ 三角すい 四角すい 円すいの体積 Powered By Line




円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題




三角柱pの体積は三角錐qの体積の何倍かという問題なのですが 求め方から忘れたのでどな Clear



三角錐とは 体積 表面積の公式や求め方 受験辞典
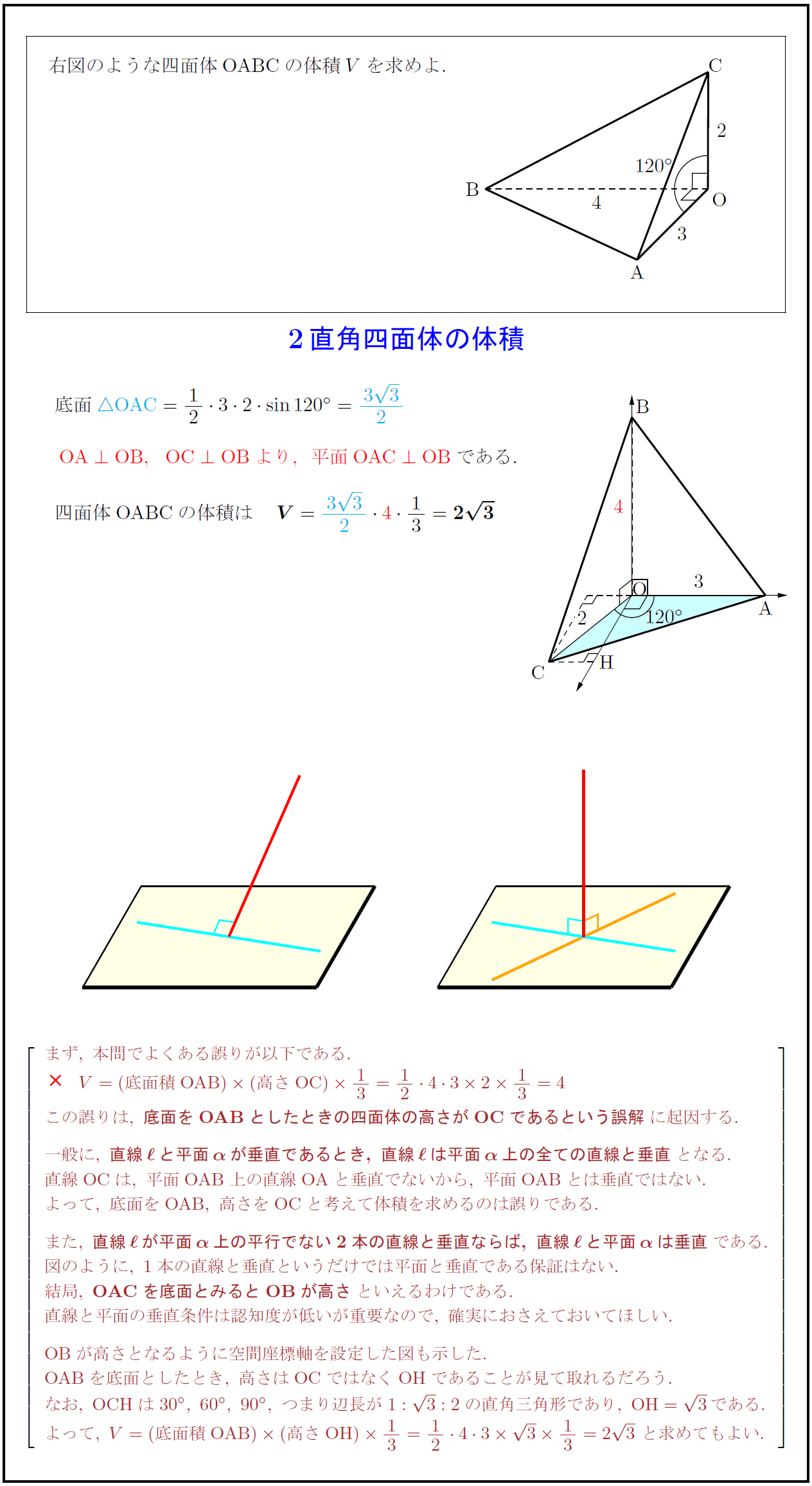



高校数学 2直角四面体の体積 直線と平面の垂直条件 受験の月



U9j580gf8iba369ji2w Xyz P 296




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




中3 三角形の相似 円錐の体積比 日本語版 Youtube



48s96ub7b0z5f Net Kuukan Bekutoru Taiseki 1
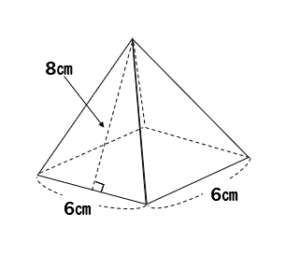



3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ



1




簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ




空間図形15 断頭三角柱の体積 Youtube
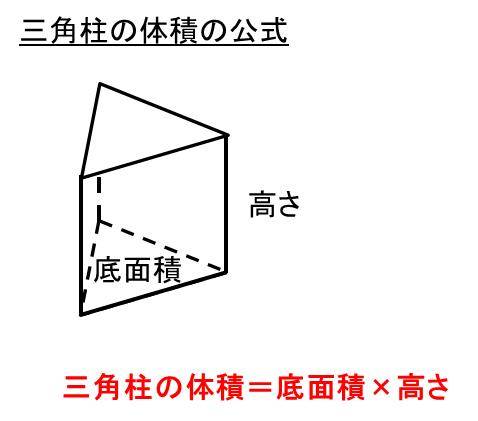



三角柱の表面積 底面積も と体積を求める公式と計算問題 単位との関係 ウルトラフリーダム
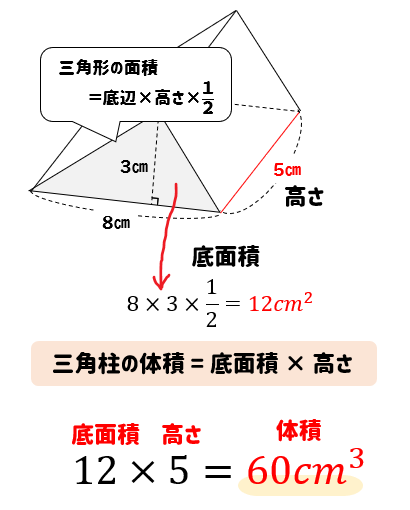



3分でなるほど 三角柱の体積 表面積の求め方をマスターしよう 数スタ




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学



三角錐の体積の公式は 1分でわかる公式 問題 底面積との関係




四角錐の体積の求め方 公式 小学生 中学生の勉強



3




円錐の体積ってなんであの公式なの Webty Staff Blog




角錐の体積の求め方 簡単な問題で公式の使い方がわかるよ 中学や高校の数学の計算問題



0 件のコメント:
コメントを投稿